Algorithms and Data Structures Cheatsheet

A quick reference guide to some of the most commonly used algorithms in DSA

Time and Space Complexity. Big O Notation#

Time Complexity

Demonstrates how fast the computing time of an algorithm escalates as the size of the input increases.

When solving problems, we can compare algorithm Time Complexity to input size and validate if given algorithm fits to input size.

Big O Notation

Analyzes asymptotic - answers how fast function grows.

Associates problem size n with processing time to solve problem t:

n - size
 
6 ┤      *
  │     *
4 ┤    *
  │   *
2 ┤  *
  └──┬──┬──┬──┬──┬──┬───
  0  1  2  3  4  5  6   t - time

Best, Worst, and Average Cases

• Best: Function performs minimal operations required to solve problem on input of n elements
• Worst: Maximum amount of steps
• Average Average amount of steps

In real-time computing, the worst-case execution time is often of particular concern since it is important to know how much time might be needed in the worst case to guarantee that the algorithm will always finish on time.

Example - Bogosort (Permutation sort)

Bogosort creates permutation of input array and checks if it's sorted.

• Best: $O_{best}(n)$ - array initially sorted, so it's needed n operations to check if each element on right place
• Worst: $O_{worst}(\infty)$ - since bogosort creates random permutation each time, in worst case it will never produce sorted permutation
• Average $O_{avg}(n \cdot n!)$ - amount of permutations is $n!$

Order of Magnitude

A description of a function in terms of Big $O$ notation typically provides only an upper bound on the growth rate of the function.

To calculate Order of Magnitude:

• Discard constants:

  • $3n^2 + 2n + 10\log n + 5$ $\to n^2 + n + \log n$

• Pick only the most significant function:

  • $n^2 + n + \log n \to n^2$

Typical Operations with Big O Notation

• Adding two functions or complexities
  • $O(n) + O(m) \to O(n + m)$ $\text{or}\;O(\max(n, m))$
• Multiplying two functions or complexities
  • $O(n) \cdot O(m) \to O(n \cdot m)$

Example $\gdef\computeTime{0.25 \cdot 10^{-9}\frac{seconds}{operation}}$

• $O(n!)$ - Time Complexity
• $4 \text{ GHz}$ - Processor single-core speed

Time calculations for n = 8 and n = 100:

• How much time it takes for 1 operation computed on $4 \text{ GHz}$ single-core processor $\rightarrow$ $4 \text{ GHz} = 4 \cdot 10^9 \frac{operations}{second}$ $\rightarrow$ $\\computeTime$
• If maximum n = 8 $\rightarrow 8! = 40320$ $\rightarrow 40320 \cdot \\computeTime$ $= 1.008×10^{−5}$ seconds. So, computer will be able to compute it in reasonable time.
• If maximum n = 100 → $100! =$ number with 158 digits $\rightarrow 100! \cdot \\computeTime$ $\approx$ $3 \cdot 10^{150}$ years. This is $\approx 2.14 \cdot 10^{140}$ times longer than our universe 🪐 exists!

Growth rate comparison

Space Complexity

Space complexity measures the memory required by an algorithm as a function of the input size

Common Space Complexities:

• $O(1)$ - constant space
• $O(n)$ - linear space, and
• $O(n^2)$ - quadratic space.

Optimizing Space complexity can lead to more efficient algorithms, especially in large-scale data processing.

Two pointers#

Iterating two pointers across an array to search for a pair of indices satisfying some condition in linear time.

Variants

• Opposite directional

  • Medium
    167. Two Sum II - Input Array Is Sorted
  • Hard
    42. Trapping Rain Water

• Same directional

  • Easy
    26. Remove Duplicates from Sorted Array

• Fast and slow pointers

  • Easy
    141. Linked List Cycle
  • Easy
    876. Middle of the Linked List

When to use

• Sequential data structure (arrays, linked lists)
• Process pairs
• Remove duplicates from a sorted data
• Detect cycle in array
• Find a pair, triplet, or a subarray that satisfies a specific condition
• Reversing, partitioning, swapping, or rearranging
• String manipulation
• Array partitioning
• Etc. like Two sum or container with water variations

Problem examples

167. Two Sum II - Input Array Is Sorted

Medium

Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number.

167. Two Sum II - Input Array Is Sorted

---

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        low = 0
        high = len(numbers) - 1
        while low < high:
            sum = numbers[low] + numbers[high]
 
            if sum == target:
                return [low + 1, high + 1]
            elif sum < target:
                low += 1
            else:
                high -= 1
        return [-1, -1]

Time Complexity

$O(n)$

Space Complexity

$O(1)$

---

876. Middle of the Linked List

Easy

Given the head of a singly linked list, return the middle node of the linked list.

If there are two middle nodes, return the second middle node.

876. Middle of the Linked List

---

class Solution:
    def middleNode(self, head):
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        return slow

Time Complexity

$O(n)$

Space Complexity

$O(1)$

---

42. Trapping Rain Water

Hard

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

42. Trapping Rain Water

---

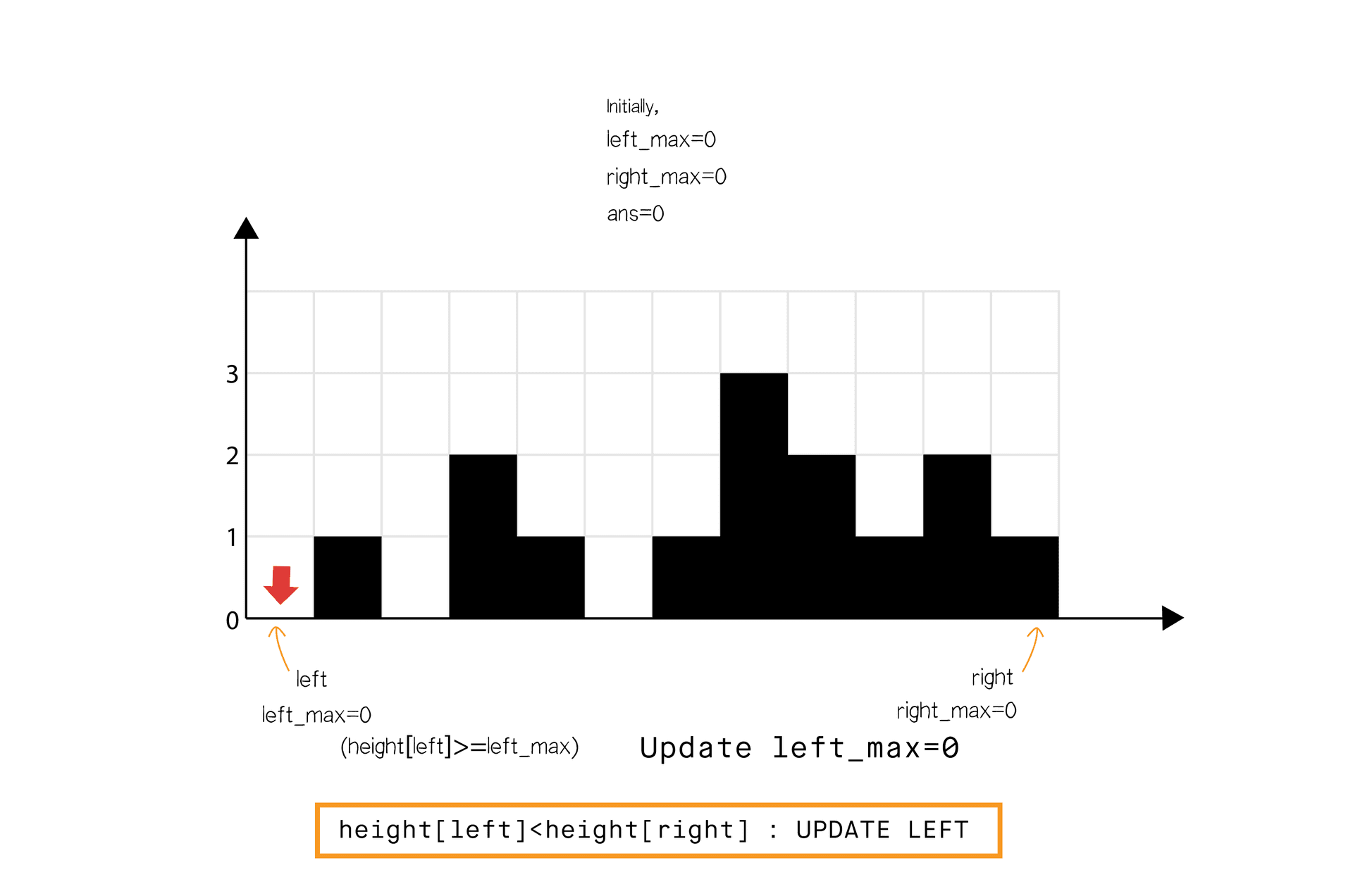
class Solution:
    def trap(self, height: List[int]) -> int:
        left, right = 0, len(height) - 1
        ans = 0
        left_max, right_max = 0, 0
        while left < right:
            if height[left] < height[right]:
                left_max = max(left_max, height[left])
                ans += left_max - height[left]
                left += 1
            else:
                right_max = max(right_max, height[right])
                ans += right_max - height[right]
                right -= 1
        return ans

Time Complexity

$O(n)$

Space Complexity

$O(1)$

Sliding window#

Maintain a dynamic window that slides through the array or string, adjusting its boundaries as needed to track relevant elements or characters.

Sliding window converts multiple nested loops into single loop, reducing the time complexity from $O(n^2)$ or $O(n^3)$ to $O(n)$.

Variants

• Fixed window size
  • Medium
    2461. Maximum Sum of Distinct Subarrays With Length K
• Variable window size
  1. Initialize window indices: Start with start and end pointers at the first element.
  2. Expand the window: Increment the end pointer to expand the window if conditions are met.
  3. Process the window: Perform required operations when the window meets criteria.
  4. Adjust the window size: Move the start pointer to adjust size and meet desired criteria.
  • Medium
    209. Minimum Size Subarray Sum
• Growing window
  • Medium
    3. Longest Substring Without Repeating Characters
  • Medium
    904. Fruit Into Baskets
• Shrinking window
• Multiple windows: Maintaining overlapping or disjoint windows can help solve problems more efficiently.
  • Hard
    992. Subarrays with K Different Integers

When to use

• Contiguous data: array, linked list, string, or stream
• Processing subsets of elements: The problem requires repeated computations on a contiguous subset of data elements (a subarray or a substring) of fixed or variable length
• Find longest, shortest or target values of a sequence

Problem patterns

1. Running Average: Efficiently calculate the average of a fixed-size window in a data stream.
2. Formulating Adjacent Pairs: Process adjacent pairs in an ordered structure for easy access and operation.
3. Target Value Identification: Adjust window size to search efficiently for specific values or subarrays.
4. Longest/Shortest/Most Optimal Sequence: Identify the desired sequence in a collection by sliding a window through it.

Problem examples

904. Fruit Into Baskets

Medium

You are visiting a farm that has a single row of fruit trees arranged from left to right. The trees are represented by an integer array fruits where fruits[i] is the type of fruit the ith tree produces.

You want to collect as much fruit as possible. However, the owner has some strict rules that you must follow:

• You only have two baskets, and each basket can only hold a single type of fruit. There is no limit on the amount of fruit each basket can hold.
• Starting from any tree of your choice, you must pick exactly one fruit from every tree (including the start tree) while moving to the right. The picked fruits must fit in one of your baskets.
• Once you reach a tree with fruit that cannot fit in your baskets, you must stop.
• Given the integer array fruits, return the maximum number of fruits you can pick.

Example:

Input: fruits = [0,1,2,2]

Output: 3

Explanation: We can pick from trees [1,2,2]. If we had started at the first tree, we would only pick from trees [0,1].

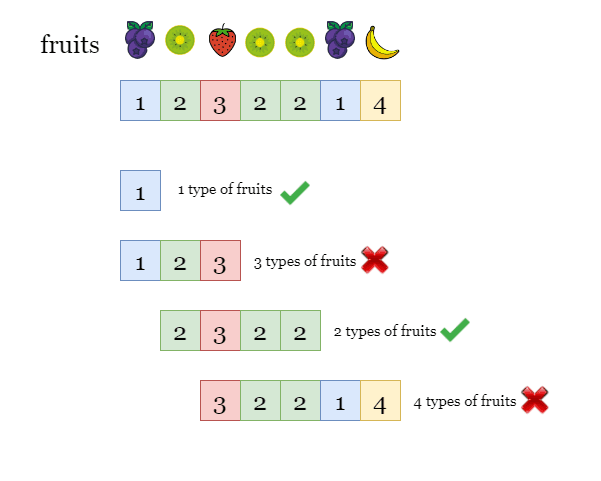
Let's compare Brute Force approach with Sliding window:

904. Fruit Into Baskets. Brute Force approach

---

class Solution:
    def totalFruit(self, fruits: List[int]) -> int:
        max_picked = 0
 
        for left in range(len(fruits)):
            basket = set()
            right = left
 
            while right < len(fruits):
                if fruits[right] not in basket and len(basket) == 2:
                    break
                basket.add(fruits[right])
                right += 1
 
            max_picked = max(max_picked, right - left)
        return max_picked

Time Complexity

$O(n^2)$

Space Complexity

$O(1)$

In second approach, two nested loops converted into a single loop thus improving Time Complexity from $O(n^2)$ to $O(n)$:

904. Fruit Into Baskets. Sliding window approach

---

class Solution:
    def totalFruit(self, fruits: List[int]) -> int:
        basket = {}
        max_picked = 0
        left = 0
 
        for right in range(len(fruits)):
            basket[fruits[right]] = basket.get(fruits[right], 0) + 1
 
            while len(basket) > 2:
                basket[fruits[left]] -= 1
                if basket[fruits[left]] == 0:
                    del basket[fruits[left]]
                left += 1
 
            max_picked = max(max_picked, right - left + 1)
        return max_picked

Time Complexity

$O(n)$

Space Complexity

$O(1)$

---

2461. Maximum Sum of Distinct Subarrays With Length K

Medium

You are given an integer array nums and an integer k. Find the maximum subarray sum of all the subarrays of nums that meet the following conditions:

• The length of the subarray is k
• All the elements of the subarray are distinct.

Return the maximum subarray sum of all the subarrays that meet the conditions. If no subarray meets the conditions, return 0.

Example:

Input: nums = [1,5,4,2,9,9,9], k = 3

Output: 15

Explanation: The subarray of length 3 with max sum of 15 is [4,2,9]

2461. Maximum Sum of Distinct Subarrays With Length K

---

class Solution:
    def maximum_subarray_sum(self, nums, k):
        res = cur_sum = 0
        last_seen_to_idx = {}
        last_seen = -1
 
        for i, num in enumerate(nums):
            cur_sum += num
            if i >= k:
                cur_sum -= nums[i - k]
            last_seen = max(last_seen, last_seen_to_idx.get(num, -1))
            if i - last_seen >= k:
                res = max(res, cur_sum)
            last_seen_to_idx[num] = i
 
        return res

Time Complexity

$O(n)$

Space Complexity

$O(n)$

---

209. Minimum Size Subarray Sum

Medium

Given an array of positive integers nums and a positive integer target, return the minimal length of a subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example:

Input: target = 7, nums = [2,3,1,2,4,3]

Output: 2

Explanation: The subarray [4,3] has the minimal length under the problem constraint.

209. Minimum Size Subarray Sum

---

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        left = 0
        right = 0
        sumOfCurrentWindow = 0
        res = float('inf')
 
        for right in range(0, len(nums)):
            sumOfCurrentWindow += nums[right]
 
            while sumOfCurrentWindow >= target:
                res = min(res, right - left + 1)
                sumOfCurrentWindow -= nums[left]
                left += 1
 
        return res if res != float('inf') else 0

Time Complexity

$O(n)$

Space Complexity

$O(1)$

---

1456. Maximum Number of Vowels in a Substring of Given Length

Medium

Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k.

Example:

Input: s = "abciiidef", k = 3

Output: 3

Explanation: The substring "iii" contains 3 vowel letters.

1456. Maximum Number of Vowels in a Substring of Given Length

---

class Solution:
    def maxVowels(self, s: str, k: int) -> int:
        vowels = set("aeiou")
        count = 0
        for i in range(k):
            count += int(s[i] in vowels)
        answer = count
        for i in range(k, len(s)):
            count += int(s[i] in vowels)
            count -= int(s[i - k] in vowels)
            answer = max(answer, count)
 
        return answer

Time Complexity

$O(n)$

Space Complexity

$O(1)$

Intervals#

Performing operations on set of intervals. Typical interval problem deals with array of overlapping intervals e.g. [[1, 3], [3, 5]].

Common tasks with intervals

• Merging intersecting intervals
  • Medium
    56. Merge Intervals
• Inserting new intervals into existing sets
  • Medium
    57. Insert Interval
• Schedule tasks
  • Medium
    621. Task Scheduler
• Arrange meeting rooms
  • Medium
    253. Meeting Rooms II
• Determining the minimum number of intervals needed to cover a given range

Corner cases

• No intervals
• Single interval
• Two intervals
• Non-overlapping intervals
• An interval totally consumed within another interval
• Duplicate intervals (exactly the same start and end)
• Intervals which start right where another interval ends - [[1, 2], [2, 3]]

When to use

• Given intervals
• Find union / intersection / gaps

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x: x[0])
        merged = []
 
        for interval in intervals:
            if not merged or merged[-1][1] < interval[0]:
                merged.append(interval)
            else:
                merged[-1][1] = max(merged[-1][1], interval[1])
 
        return merged

class Solution:
    def insert(
        self, intervals: List[List[int]], newInterval: List[int]
    ) -> List[List[int]]:
        # If the intervals vector is empty, return a vector containing the newInterval
        if not intervals:
            return [newInterval]
 
        n = len(intervals)
        target = newInterval[0]
        left, right = 0, n - 1
 
        # Binary search to find the position to insert newInterval
        while left <= right:
            mid = (left + right) // 2
            if intervals[mid][0] < target:
                left = mid + 1
            else:
                right = mid - 1
 
        # Insert newInterval at the found position
        intervals.insert(left, newInterval)
 
        # Merge overlapping intervals
        res = []
        for interval in intervals:
            # If res is empty or there is no overlap, add the interval to the result
            if not res or res[-1][1] < interval[0]:
                res.append(interval)
            # If there is an overlap, merge the intervals by updating the end of the last interval in res
            else:
                res[-1][1] = max(res[-1][1], interval[1])
        return res

class Solution:
    def leastInterval(self, tasks: List[str], n: int) -> int:
        counter = Counter(tasks)
        max_heap = [-val for val in counter.values()]
        heapify(max_heap)
        res = 0
        while max_heap:
            cycle = n + 1
            tasks = []
            while cycle and max_heap:
                task = -heappop(max_heap)
                cycle -= 1
                if task > 1:
                    tasks.append(-(task - 1))
            while tasks:
                heappush(max_heap, tasks.pop())
            res += n + 1 if max_heap else n - cycle + 1
 
        return res

class Solution:
    def minMeetingRooms(self, intervals: List[List[int]]) -> int:
        intervals.sort()
        end_times = []
        for start, end in intervals:
            if not end_times or end_times[0] > start:
                heapq.heappush(end_times, end)
            else:
                heapq.heapreplace(end_times, end)
 
        return len(end_times)

Linked List#

This section focuses on in-place operations with Linked Lists.

Properties

• Sequential data structure (like array, unlike tree)
• Slow access, but fast add / delete operations

Variants

• Singly-linked list

┌─────┐     ┌─────┐     ┌─────┐
│  A  ├────►│  B  ├────►│  C  ├────►null
└─────┘     └─────┘     └─────┘

• Doubly-linked list

         ┌─────┐     ┌─────┐     ┌─────┐
null◄────┤  A  │◄───►│  B  │◄───►│  C  ├────►null
         └─────┘     └─────┘     └─────┘

• Circular-linked list

┌─────┐     ┌─────┐     ┌─────┐
│  A  ├────►│  B  ├────►│  C  │
└─────┘     └─────┘     └─────┘
   ▲                       │
   └───────────────────────┘

Example of Singly-linked List

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next
 
first_node = ListNode(1)
second_node = ListNode(2)
 
first_node.next = second_node

┌─────┐    ┌─────┐
│  1  ├───►│  2  ├───►null
└─────┘    └─────┘

Dummy node technique

If operation is going to be performed on head or tail node, we can create dummy node, and point dummy.next to head. It helps not to handle edge cases for head only:

dummy = ListNode()
dummy.next = head
 
# perform operations on dummy.next
# we don't need to handle head specifically
 
return dummy.next

Typical operations with Linked Lists

• List Node operations
  • Swap nodes
    Medium
    1721. Swapping Nodes in a Linked List
  • Remove node
    Medium
    237. Delete Node in a Linked List
• Whole List operations
  • Reverse
    Easy
    206. Reverse Linked List
  • Reorder
    Medium
    143. Reorder List
  • Split
    Medium
    725. Split Linked List in Parts
  • Merge 2 or more lists
    Hard
    23. Merge k Sorted Lists
• Search
  • Find middle
    Easy
    206. Reverse Linked List
  • Find cycle
    Easy
    141. Linked List Cycle
• Custom data structures with Linked List under the hood
  • Medium
    146. LRU Cache
  • Hard
    460. LFU Cache

When to use

• Linked list restructuring: The input data is given as a linked list, and the task is to modify its structure without modifying the data of the individual nodes.
• In-place modification: The modifications to the linked list must be made in place, that is, we’re not allowed to use more than $O(1)$ additional space.

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        prev = None
        curr = head
        while curr:
            next_temp = curr.next
            curr.next = prev
            prev = curr
            curr = next_temp
 
        return prev

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        if (not head) or (not head.next):
            return head
 
        p = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return p

┌─────┐    ┌─────┐    ┌─────┐
│  1  ├───►│  2  ├───►│  3  ├─┐
└─────┘    └─────┘    └─────┘ │
  ▲                           │
  └───────────────────────────┘

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if head is None:
            return False
        slow = head
        fast = head.next
        while slow != fast:
            if fast is None or fast.next is None:
                return False
            slow = slow.next
            fast = fast.next.next
        return True

1. Initial list:
┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐
│  1  ├───►│  2  ├───►│  3  ├───►│  4  ├───►│  5  ├───►null
└─────┘    └─────┘    └─────┘    └─────┘    └─────┘
 
1. Find middle (middle points to 3):
┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐
│  1  ├───►│  2  ├───►│  3  ├───►│  4  ├───►│  5  ├───►null
└─────┘    └─────┘    └─────┘    └─────┘    └─────┘
                         ▲
                      middle
 
1. Reverse second half (4->5 becomes 5->4):
┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐
│  1  ├───►│  2  ├───►│  3  ├───►│  4  ◄────│  5  │
└─────┘    └─────┘    └─────┘    └─────┘    └─────┘
                                             prev
 
1. Start merging (first=1, second=5):
┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐
│  1  ├─┐  │  2  ├───►│  3  ├───►│  4  ◄────│  5  │
└─────┘ │  └─────┘    └─────┘    └─────┘    └─────┘
        │                                       ▲
        └───────────────────────────────────────┘
 
1. Final reordered list:
┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐    ┌─────┐
│  1  ├───►│  5  ├───►│  2  ├───►│  4  ├───►│  3  ├───►null
└─────┘    └─────┘    └─────┘    └─────┘    └─────┘

class Solution:
    def reorderList(self, head: ListNode) -> None:
        if not head:
            return
 
        # find the middle of linked list [Problem 876]
        # in 1->2->3->4->5->6 find 4
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
 
        # reverse the second part of the list [Problem 206]
        # convert 1->2->3->4->5->6 into 1->2->3->4 and 6->5->4
        # reverse the second half in-place
        prev, curr = None, slow
        while curr:
            curr.next, prev, curr = prev, curr, curr.next
 
        # merge two sorted linked lists [Problem 21]
        # merge 1->2->3->4 and 6->5->4 into 1->6->2->5->3->4
        first, second = head, prev
        while second.next:
            first.next, first = second, first.next
            second.next, second = first, second.next

Heap: Introduction#

Heap is a complete binary tree where each node is smaller than its children (for min heap). This property is called Heap invariant, heap must always comply to it.

Priority Queue vs Heap

• Priority queue
  • Abstract data structure (like stack or queue) that behaves like queue (First In, First Out)
  • Each element has priority - the higher propriety element comes first
  • Specifies behavior of data structure
  • Doesn't define internal implementation
• Heap
  • Implements of Priority queue

Variants

• Min heap - each parent node smaller of equal to its children
• Max heap - each parent node bigger or equal to its children

Operations on heap

• Add node
  1. Add new node to end of heap
  2. Swap the node with parent if it's bigger than parent
  3. At most, $O(\log n)$ swaps could be made since heap - Complete binary tree. In complete binary tree, height = $\log n$
• Remove node
  1. Take tree root and remove it from tree
  2. Place last element to root
  3. Swap with children to achieve Heap invariant
  4. At most, $O(\log n)$ swaps could be made
• Heapify
  1. Start from last leave
  2. If node doesn't satisfy Heap invariant, recursively heapify subtree
  3. Move up the tree until the entire tree satisfies the Heap invariant
  4. The total amount of swaps is $O(n)$

Array representation of Heap

Heap usually represented as array:

• Node_i stored in array by index i
• Node_i left and right children could be found by index 2 * i and 2 * i + 1
• It's convenient to store nodes starting from index 1

Example or Max heap

Tree representation:

Complete binary tree of height 2
 
Level             Tree
 
  0:                9
                  /   \
  1:             7     8
                /
  2:           5 - all levels are filled except for last layer

Array representation with indices:

          0 index is blank because 0 * 2 = 0
          ↓
        ┌───┬───┬───┬───┬───┐
Value   │ - │ 9 │ 7 │ 8 │ 5 │
        └───┴───┴───┴───┴───┘
Index     0   1   2   3   4

When to use

• K-th element

  • Medium
    Kth Largest Element in an Array (Problem 215)
  • Medium
    Kth Smallest Element in a Sorted Matrix (Problem 378)

• Top K elements

  • Medium
    Top K Frequent Elements (Problem 347)
  • Medium
    K Closest Points to Origin (Problem 973)

• Heap sort

  • Medium
    Sort an Array (Problem 912)

• Sort subset of elements resulting to TC optimization from $O(n\cdot\log n)$ to $O(n\cdot\log k)$ where k is heap size

  • Medium
    Find K Pairs with Smallest Sums (Problem 373)
  • Hard
    Merge k Sorted Lists (Problem 23)

class Solution:
    def findKthLargest(self, nums, k):
        heap = []
        for num in nums:
            heapq.heappush(heap, num)
            if len(heap) > k:
                heapq.heappop(heap)
 
        return heap[0]

class Solution:
   def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:
       heap, seen, res = [(nums1[0] + nums2[0], 0, 0)], {(0, 0)}, []
       while heap and len(res) < k:
           _, i, j = heappop(heap)
           res.append([nums1[i], nums2[j]])
           for i2, j2 in [(i, j + 1), (i + 1, j)]:
               if i2 < len(nums1) and j2 < len(nums2) and (i2, j2) not in seen:
                   seen.add((i2, j2))
                   heappush(heap, (nums1[i2] + nums2[j2], i2, j2))
       return res

Heap: Two heaps#

Two heaps approach used to find out middle of moving dataset

• Hard
  295. Find Median from Data Stream
• Hard
  480. Sliding Window Median

It assumes having

• Max heap to store maximum of part of dataset
• Min heap to store minimum of part of dataset

Algorithm for finding median of k-size dataset

• Initialization - placing elements to heaps by $O(k\cdot\log k)$
  1. Initialize min heap and max heap
     • Min heap will store elements right to the median (bigger)
     • Max heap will store elements left to the median (smaller)
  2. Place every item in min heap
  3. If min heap size exceeds k // 2
     • Pop element from min heap (it will be smallest one)
     • Place to max heap
• Find median - $O(1)$
  • k even - Average of min heap and max heap roots
  • k odd - Max heap root
• Shift sliding window
  • Perform steps 2-3

When to use

• Linear data: The input data is linear but not sorted
• Stream of data
• Find Max / Min:
  • Find maximums / minimums / maximum and minimum of 2 datasets

class Solution:
    def findMaximizedCapital(
        self, k: int, w: int, profits: List[int], capital: List[int]
    ) -> int:
        min_capitals = [(c, p) for c, p in zip(capital, profits)]
        heapq.heapify(min_capitals)
        max_profits = []
        for _ in range(k):
            while min_capitals and min_capitals[0][0] <= w:
                c, p = heapq.heappop(min_capitals)
                heapq.heappush(max_profits, -p)
            if max_profits:
                w += -heapq.heappop(max_profits)
        return w

Window position                Median
---------------                -----
[1  3  -1] -3  5  3  6  7        1
 1 [3  -1  -3] 5  3  6  7       -1
 1  3 [-1  -3  5] 3  6  7       -1
 1  3  -1 [-3  5  3] 6  7        3
 1  3  -1  -3 [5  3  6] 7        5
 1  3  -1  -3  5 [3  6  7]       6

class Solution:
    def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:
        def clean(h, is_min):
            while h and rm.get(h[0] if is_min else -h[0], 0):
                rm[h[0] if is_min else -h[0]] -= 1
                heapq.heappop(h)
 
        rm, lo, hi, res = {}, [], [], []
        for i in range(k):
            heapq.heappush(lo, -nums[i])
        for _ in range(k // 2):
            heapq.heappush(hi, -heapq.heappop(lo))
 
        for i in range(k, len(nums) + 1):
            res.append(-lo[0] if k % 2 else (-lo[0] + hi[0]) / 2)
            if i == len(nums):
                break
 
            out, in_num = nums[i - k], nums[i]
            rm[out] = rm.get(out, 0) + 1
            bal = -1 if out <= -lo[0] else 1
 
            if lo and in_num <= -lo[0]:
                heapq.heappush(lo, -in_num)
                bal += 1
            else:
                heapq.heappush(hi, in_num)
                bal -= 1
 
            if bal < 0:
                heapq.heappush(lo, -heapq.heappop(hi))
            if bal > 0:
                heapq.heappush(hi, -heapq.heappop(lo))
            clean(lo, False)
            clean(hi, True)
 
        return res

Heap: Top K Elements#

The top k elements pattern is crucial for efficiently finding a specific number of elements, k, from a dataset.

Maintains a heap of size k while iterating through the list of elements.

Time Complexity

Without this pattern, sorting the whole collection is $O(n \cdot \log n)$, plus $O(k)$ to pick top k elements. The top k pattern achieves $O(n \cdot \log k)$ by selectively tracking compared elements, using a heap.

Using Heap

A heap is ideal for managing the smallest or largest k elements. By using a max heap for smallest elements and a min heap for largest, we can maintain ordered elements with quick access to the smallest or largest.

Operating Procedure

1. Insert first k elements into the appropriate heap.
   • Min heap for largest elements.
   • Max heap for smallest elements.
2. For remaining elements:
   • In min heap (for largest elements), replace the smallest (top) with any found larger element.
   • In max heap (for smallest elements), replace the largest (top) with any found smaller element.

Efficiency

Time complexity of Top K approach using heap:

• $O(\log k)$ - insertions and removals
• $O(n\cdot\log k)$ - processing all elements
• $O(k\cdot\log k)$ - retrieving all k elements, due to reorganization after each removal.

Time complexity comparison

n - number of all items. k - top k elements

• Brute force - $O(n\cdot k)$
• Sorting - $O(n \cdot \log n)$
• Heap - $O(n \cdot \log k)$

Typical problems

• Easy
  703. Kth Largest Element in a Stream
• Medium
  767. Reorganize String
• Medium
  973. K Closest Points to Origin

When to use

• Unsorted List Analysis: Task involves extracting a specific subset (largest, smallest, most/least frequent) from an unsorted list, either as the final goal or an intermediate step.
• Identifying a Specific Subset: To identify a subset based on criteria like top k, kth largest/smallest, or k most frequent, indicating the top k elements pattern is a fit.

How to identify Top K pattern

• Top k element
• Smallest / Biggest element
• Most / Least frequent k elements
• Furthest / Nearest
• Given Unsorted data

Pitfalls

• Sometimes mathematical approach faster
• Sometimes other patterns faster: Top K Frequent Elements
  • Quickselect - Average Time Complexity $O(n)$
  • Heap - Average Time Complexity $O(n \cdot \log k)$
• If data is sorted, use binary search or others
• If need to find one extremum, heap is not needed

Problem examples

347. Top K Frequent Elements

Medium

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Example:

Input: nums = [1,1,1,2,2,3], k = 2

Output: [1,2]

347. Top K Frequent Elements

---

class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        heap = []
        for num, freq in Counter(nums).items():
            heapq.heappush(heap, (freq, num))
            if len(heap) > k:
                heapq.heappop(heap)
        return [num for freq, num in heap]

Time Complexity

$O(n\cdot \log k)$

Space Complexity

$O(n + k)$

---

767. Reorganize String

Medium

Given a string s, rearrange the characters of s so that any two adjacent characters are not the same.

Return any possible rearrangement of s or return "" if not possible.

Example:

Input: s = "aab"

Output: "aba"

767. Reorganize String

---

class Solution:
    def reorganizeString(self, s: str) -> str:
        ans = []
        pq = [(-count, char) for char, count in Counter(s).items()]
        heapify(pq)
 
        while pq:
            count_first, char_first = heappop(pq)
            if not ans or char_first != ans[-1]:
                ans.append(char_first)
                if count_first + 1 != 0:
                    heappush(pq, (count_first + 1, char_first))
            else:
                if not pq: return ''
                count_second, char_second = heappop(pq)
                ans.append(char_second)
                if count_second + 1 != 0:
                    heappush(pq, (count_second + 1, char_second))
                heappush(pq, (count_first, char_first))
 
        return ''.join(ans)

Time Complexity

$O(n\cdot \log k)$

Space Complexity

$O(k)$

---

973. K Closest Points to Origin

Medium

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x1 - x2)2 + (y1 - y2)2).

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

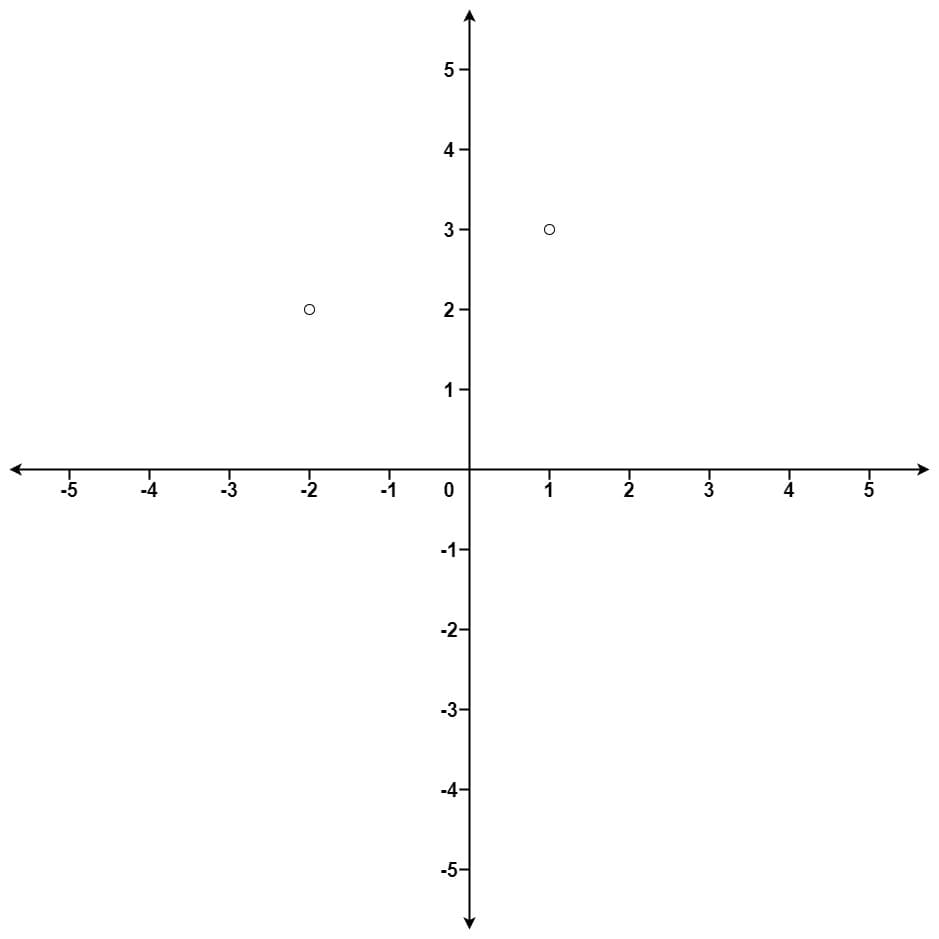
Example:

Input: points = [[1,3],[-2,2]], k = 1

Output: [[-2,2]]

Explanation: explanation: "The distance between (1, 3) and the origin is sqrt(10). The distance between (-2, 2) and the origin is sqrt(8). Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin. We only want the closest k = 1 points from the origin, so the answer is just [[-2,2]].

973. K Closest Points to Origin

---

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        dist_idx_heap = []
        for i, (x, y) in enumerate(points):
            dist = sqrt(x**2 + y**2)
            heapq.heappush(dist_idx_heap, (-dist, i))
            if len(dist_idx_heap) > k:
                heapq.heappop(dist_idx_heap)
        res = []
        for dist, i in dist_idx_heap:
            res.append(points[i])
        return res

Time Complexity

$O(n\cdot \log k)$

Space Complexity

$O(k)$

Heap: K-Way Merge#

The K-way merge pattern combines k sorted data structures into a single sorted output.

It works by repeatedly selecting the smallest (or largest) element from among the first elements of each input list and adding it to the output list, continuing until all elements are merged in order.

K-way merge of sorted data could be achieved by:

• Heaps
• Merge sort

Min Heap Approach:

1. Insert first element from each list into min heap
2. Remove heap's top element, add to output
3. Replace with next element from same input list
4. Repeat until all elements merged

Divide & Merge (merge sort):

1. Divide lists into 2 parts and merge each part
2. Continue dividing and merging resulting lists
3. Repeat until single sorted list remains

Typical problems

• Medium
  378. Kth Smallest Element in a Sorted Matrix
• Medium
  373. Find K Pairs with Smallest Sums
• Hard
  23. Merge k Sorted Lists

When to use

• Merging sorted arrays/matrix rows/columns into a single sorted sequence
• Finding kth smallest/largest element across multiple sorted collections (like finding median in multiple sorted arrays)

class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        min_heap = [(row[0], i, 0) for i, row in enumerate(matrix)]
        heapify(min_heap)
 
        while k:
            val, i, j = heappop(min_heap)
            k -= 1
            if j + 1 < len(matrix):
                heappush(min_heap, (matrix[i][j + 1], i, j + 1))
 
        return val

class Solution:
    def kSmallestPairs(
        self, nums1: List[int], nums2: List[int], k: int
    ) -> List[List[int]]:
        heap, seen, res = [(nums1[0] + nums2[0], 0, 0)], {(0, 0)}, []
        while heap and len(res) < k:
            _, i, j = heappop(heap)
            res.append([nums1[i], nums2[j]])
            for i2, j2 in [(i, j + 1), (i + 1, j)]:
                if i2 < len(nums1) and j2 < len(nums2) and (i2, j2) not in seen:
                    seen.add((i2, j2))
                    heappush(heap, (nums1[i2] + nums2[j2], i2, j2))
        return res

class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        head = cur = ListNode()
        heap = []
        for i, node in enumerate(lists):
            if not node:
                continue
            heappush(heap, (node.val, i))
        while heap:
            val, min_node_idx = heappop(heap)
            min_node = lists[min_node_idx]
            cur.next, cur = min_node, min_node
            if min_node.next:
                lists[min_node_idx] = min_node.next
                heappush(heap, (min_node.next.val, min_node_idx))
        return head.next

Binary search#

Searching algorithm in sorted array

1. It works by repeatedly dividing the search interval in half.
   1. If the target value is less than the middle element, the search continues in the left half;
   2. if greater, it continues in the right half.
2. This process is repeated until the target is found or the interval is empty.

Simple implementation

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
 
    while left <= right:
        mid = (left + right) // 2
 
        if arr[mid] == target:
            return mid  # Target found at index mid
        elif arr[mid] < target:
            left = mid + 1  # Discard the left half
        else:
            right = mid - 1  # Discard the right half
 
    return -1  # Target not found

Modified Binary search

• Modification of Binary search
• Uses same core conception of dividing search space by 2
• Applies specific conditions or transformations to address unique problems:

Variants

1. Binary Search on a Modified Array
   • Array is altered
   • Medium
     33. Search in Rotated Sorted Array - sorted and then rotated.
2. Binary Search with Multiple Requirements
   • Adapt the comparison logic to meet multiple conditions
   • Finding a range of targets
   • Identifying the leftmost or rightmost occurrences of a value
3. Finding Conditions
   • Identify boundary conditions
   • Easy
     278. First Bad Version - locating the first instance that meets a specific criterion.

These modifications allow binary search to efficiently tackle a broader range of problems.

Typical problems

• Sorted array
  • Find value
  • Find range
    • Medium
      34. Find First and Last Position of Element in Sorted Array
• Sorted array is modified (rotated)
  • Medium
    33. Search in Rotated Sorted Array
  • Medium
    153. Find Minimum in Rotated Sorted Array
• Custom comparison (good/bad version)
  • Easy
    374. Guess Number Higher or Lower
  • Easy
    278. First Bad Version
  • Medium
    162. Find Peak Element
• Task can be represented by sorted data
  • Easy
    69. Sqrt(x)
• Sorted Matrix
• Find insertion point

Comparison with other algorithms

When to use

• Time Complexity constraint - $O(\log n)$
• Linear data structure with random access
• Data is sorted
• Data structure that supports direct addressing: array, matrix
• There's no linear data structure, but data is in sorted order
  • Easy
    278. First Bad Version

Challenges using Binary Search

• Identify pattern
• Find proper condition
• Not to fall into infinite loop

Notes

• Pre-processing might be needed
  • Sort if collection is unsorted
  • Precompute if needed
    • Medium
      162. Find Peak Element
      • Precompute cumulative sum
• Sometimes we don't want to check found element in loop

while lo < hi:
    mid = (lo + hi) // 2
    if a[mid] < x:
        lo = mid + 1
    else:
        hi = mid
return lo

• Beware overflow:

mid = left + (right - left) // 2
# vs
mid = (right + left) // 2

• Sometimes we can use built-in b-search like bisect_left in Python
• Infinite loop:

while l <= r:
  ...
  l = mid

Problem examples

50. Pow(x, n)

Medium

Implement pow(x, n), which calculates x raised to the power n (i.e., xn).

Example:

Input: fruits = [0,1,2,2]

Output: 3

Explanation: We can pick from trees [1,2,2]. If we had started at the first tree, we would only pick from trees [0,1].

Brute Force

50. Pow(x, n) - Brute Force

---

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n == 0:
            return 1
        if n < 0:
            return 1 / pow(x, -n)
        return x * pow(x, n - 1)

Time Complexity

$O(n)$

Space Complexity

$O(1)$

Binary search - Recursive

50. Pow(x, n) - Binary search - Recursive

---

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n < 0:
            return 1 / self.myPow(x, -n)
        if n == 0:
            return 1
        if n % 2:
            return x * self.myPow(x, n - 1)
        return self.myPow(x * x, n / 2)

Time Complexity

$O(\log n)$

Space Complexity

$O(\log n)$

Binary search - Iterative

50. Pow(x, n) - Binary search - Iterative

---

class Solution:
    def binaryExp(self, x: float, n: int) -> float:
        if n == 0:
            return 1
 
        if n < 0:
            n = -1 * n
            x = 1.0 / x
 
        result = 1
        while n != 0:
            if n % 2 == 1:
                result *= x
                n -= 1
            x *= x
            n //= 2
        return result

Time Complexity

$O(\log n)$

Space Complexity

$O(1)$

---

162. Find Peak Element

Medium

A peak element is an element that is strictly greater than its neighbors.

Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.

You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.

You must write an algorithm that runs in $O(\log n)$ time.

Example:

Input: nums = [1,2,3,1]

Output: 2

Explanation: 3 is a peak element and your function should return the index number 2.

Input array - [1, 2, 3, 2]

Input array - [1, 2, 3]

Brute Force

162. Find Peak Element - Brute force

---

def findPeakElement(nums):
    for i in range(len(nums) - 1):
        if nums[i] > nums[i + 1]:
            return i
    return len(nums) - 1

Time Complexity

$O(n)$

Space Complexity

$O(1)$

Binary search - Iterative

Hints:

• Local peak, not global
• Items behind array borders (behind first and last) are smaller than boundary items (first and last)

162. Find Peak Element - Binary search - Iterative

---

def findPeakElement(self, nums):
    l, r = 0, len(nums) - 1
    while l < r:
        mid = (l + r) // 2
        if nums[mid] > nums[mid + 1]:
            r = mid
        else:
            l = mid + 1
    return l

Time Complexity

$O(\log n)$

Space Complexity

$O(1)$

Dynamic Programming#

Dynamic programming is a computer programming technique where an algorithmic problem is first broken down into sub-problems, the results are saved, and then the sub-problems are optimized to find the overall solution.

When to use

• The problem can be divided by subproblems
• The subproblems are overlapping

3 main components:

1. State - stores answer for i-th subproblem
2. Transition between states - how to get new solution based on previously calculated
3. Base case - what's initial or the most atomic subproblem

Approaches

• Top-Down - try to solve main problem first, and to solve it solve subproblems recursively up to base case

• Bottom-Up - solve subproblems starting from the next one to base case and finishing on main problem

• Push DP - update future states based on the current state

• Pull DP - calculate the current state based on past states

Top-Down vs Bottom-Up

Top-Down

• Benefits: Easier to implement because of recursion
• Drawbacks: Could not be appliciable because of call stack overflow

Bottom-Up

• Benefits: No recursion. Sometimes is better in space than Top-Down
• Drawbacks: Harder to implement

Hints on using DP

• Think of Base case
• First try recursive Top-Bottom
• Then if Top-Bottom doesn't fit (because of recursive stack or to optimise space, or whatsoever) then try Bottom-Up

Bitwise operations#

Operators

• AND & - Return 1 if left and right are 1
• OR | - Return 1 if left or right are 1
• XOR ^ - Return 1 if either left or right bit is 1, but not both
• NOT ~ - Inverts bits: 1 → 0, 0 → 1
  • ~n == -n - 1.
    • Example: ~1 == -2
  • arr[~k] - access kth element in array from the end:

arr = [0, 1, 2, 3, 4, 5, 6]
k = 1
arr[~k] # 5; returns second element form the end because ~1 == -2

• Bitwise shift left <<:
  • Shifts all bits of a number to the left by a specified number of positions.
  • Any bits that exceed the size of the number (e.g., 32-bit int) are discarded.
    • Example: $11_{10} \ll 3 \rightarrow 1011_{2} \ll 3 = 1011\mathbf{000}_{2} = 88_{10}$
  • $n\ll k = n * 2^k$
    • Example: $5\ll 3 = 5 * 2^3 = 40$
      • $5_{10} = 00000101_{2}$
      • $5 \ll 3 = 00000101_{2} \ll 3 = 00101\mathbf{000}_{2} = 40_{10} \\[5pt]$
• Bitwise shift right >>
  • Shift all bits to right
  • All bits on right which exceed number size are discarded
  • $n \gg 1$ - same as integer division by $2$: $n // 2$
  • $n \gg k$ - same as integer division by $k$: $n // 2^k$
  • $\operatorname{\,//\,}$
  • Example:
    • $11_{10} = 1011_{2}$
    • $11_{10} \ll 3 = 1011_{2} \ll 3 = 1011\mathbf{000}_{2}$

Comparison of bitwise operations

      1 0    1 1
    ┌────────────
AND │  0      1
OR  │  1      1
XOR │  1      0

Operations precedence

1. ~
2. >>, <<
3. &
4. ^
5. |

Example

$m \ll n \; \& \;\sim k\; |\; l \to$ $\overset{4}{\overbrace{\bigg(\overset{3}{\overbrace{\Big(\overset{2}{\overbrace{(m \ll n)}} \; \& \; \overset{1}{\overbrace{(\sim k)}}}\Big)}\; |\; l\bigg)}}$

Common operations

• Make bitmask with all 1's of length n (for n = 4, mask = 0b1111):
  • 1 << n - 1
  • ~(~0 << n)
  • ~- 2 ** n:
    1. 2 ** n - Same with 1 << n
    2. - - Make negative number.Remember, negatives are stored as Two-s complement c = ~n + 1
    3. ~ - Since complement inverts bits, we revert them back
• Check if n has at least same 1s as k:
  • n & k == k
• Set n-th bit with 1:
  • num = num & 1 << n
• Set n-th bit with 0:
  • num = num & ~(1 << n)